为什么正则化能够降低过拟合
我们通过实验发现正则化能帮助减少过拟合。这是令人高兴的事,然而不幸的是,我们没有明显的证据证明为什么正则化可以起到这个效果!一个大家经常说起的解释是:在某种程度上,越小的权重复杂度越低,因此能够更简单且更有效地描绘数据,所以我们倾向于选择这样的权重。尽管这是个很简短的解释,却也包含了一些疑点。让我们来更加仔细地探讨一下这个解释。假设我们要对一个简单的数据集建立模型:
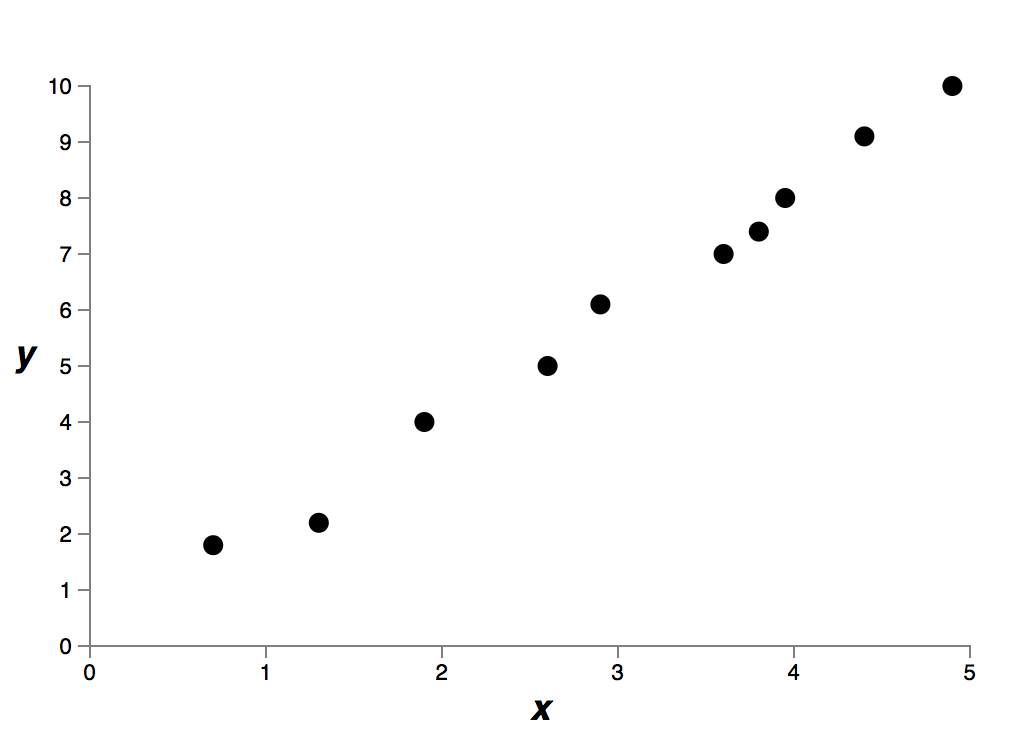
这个数据是现实世界某个问题提取得到的 和 。我们的目标是构建一个模型,得到基于 的能预测 的函数。我们可以尝试使用神经网络来构建模型,但是我将使用更简单的方法:我将把 建模为关于 的多项式。我们将使用这种方法来代替神经网络,因为多项式模型十分透明。一旦我们理解了多项式的情况,我们就可以把它迁移到神经网络上。现在,在上图中有十个点,这意味着我们可以找到一个 次多项式 来精确拟合这些数据。这是该多项式的图像:
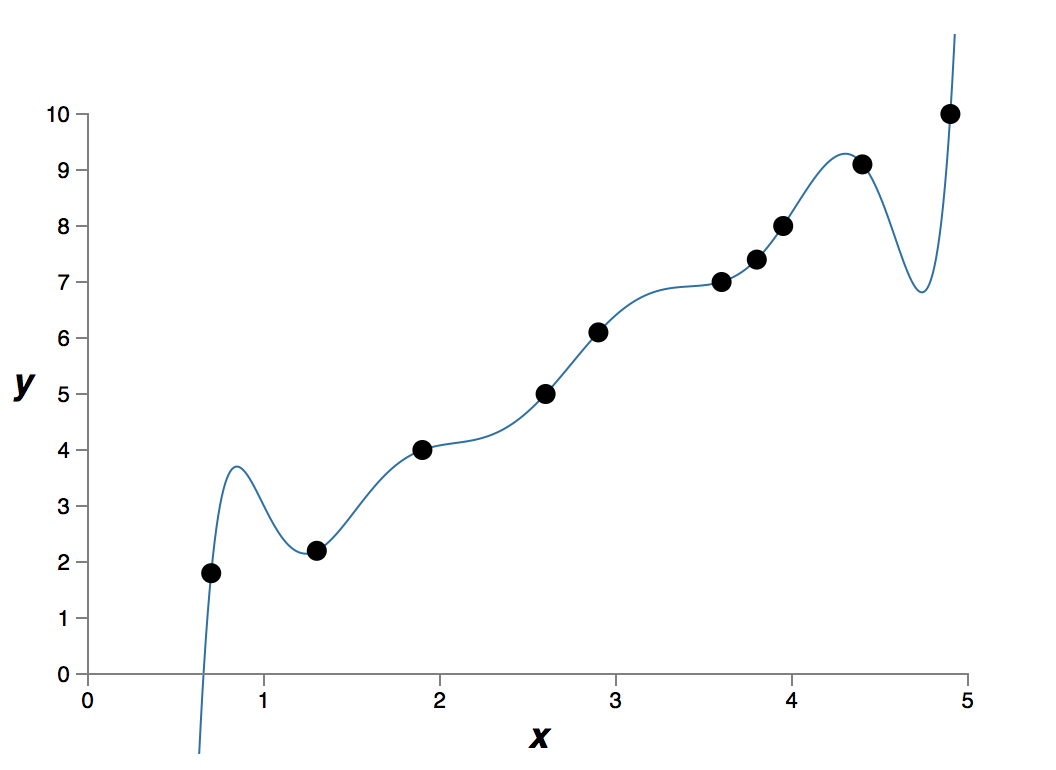
它精确拟合了数据。但是我们也可以使用线性模型 来得到一个较好的拟合:
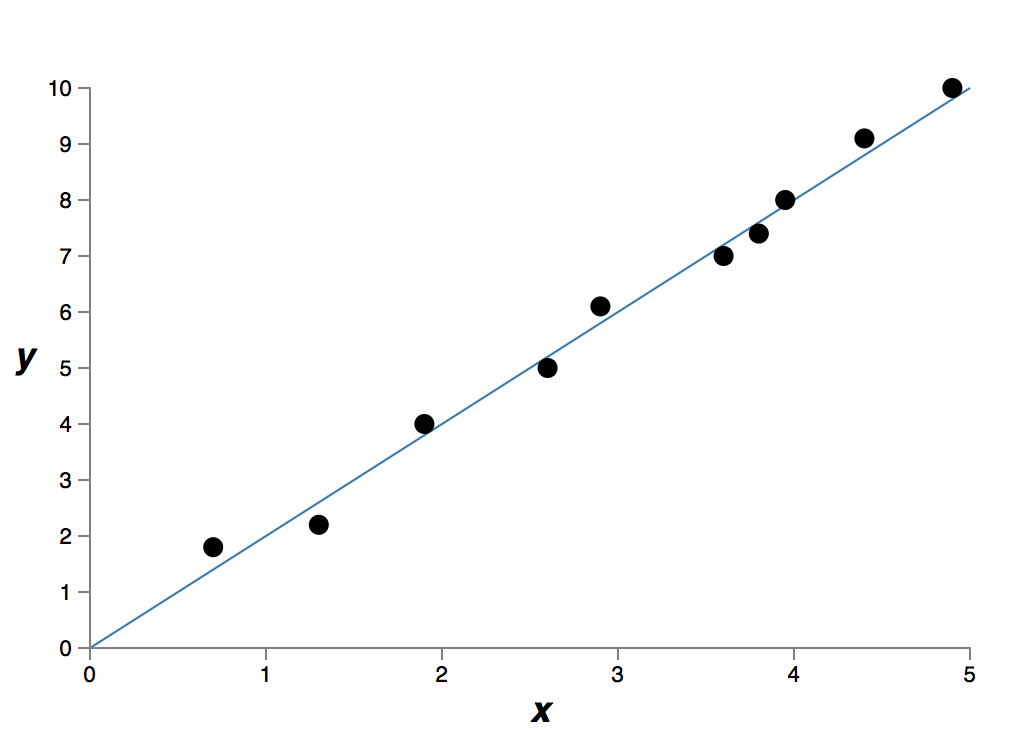
这两个哪个才是更好的模型呢?哪个更贴近真实情况?另外哪个模型能更好地泛化该问题的其它数据呢?
这些问题很难回答。事实上,如果没有足够多关于现实情况的信息时,我们很难回答任何一个问题。但是让我们考虑两种可能性:(1) 次多项式事实上真正描述了现实情况,因此这个模型可以完美泛化;(2)正确的模型是 ,但是实验中有一些因为测量误差引入的额外的噪声,也因此这个模型没有完美拟合。
确定这两种可能(可能还有第三种可能存在)哪一个正确的是不能先验的。逻辑上讲,任何一个都可能是正确的。并且这两者的差异并非微不足道。我们承认如果只关注提供的数据集,这两个模型只有很细微的差别。但是如果我们想在比我们之前展示的任何一张图都多得多的 上,预测 的值,那么两个模型的预测结果将有巨大的差异, 次多项式模型将主要由 项决定,而线性模型依旧还是线性。
有一种看法是,在科学上,除非迫不得已,我们都应该用更简单的解释。当我们找到一个看起来能解释很多数据点的简单的模型的时候我们会忍不住大喊「找到啦!」。毕竟一个简单的解释的出现似乎不可能仅仅是因为巧合,我们猜测这个模型一定表达了关于这个现象的一些潜在真理。在我们的情况中,模型 看起来要比 更简单。这种简单的模型的意外出现令人吃惊,我们也因此猜测 表达了一些潜在的真理。基于这种观点,9 次模型真的只是学习到了一些局部噪声的影响。因此当 9 次模型完美拟合了这一特定数据集的时候,这个模型不能很好泛化到其它数据集上,所以包含噪声的线性模型在预测中会有更好的表现。
我们来看看这种观点对神经网络来说意味着什么。设想我们的网络大部分都有较小的权重,正如在正则化网络中常出现的那样。小权重意味着网络的行为不会因为我们随意更改了一些输入而改变太多。这使得它不容易学习到数据中局部噪声。可以把它想象成一种能使孤立的数据不会过多影响网络输出的方法,相反地,一个正则化的网络会学习去响应一些经常出现在整个训练集中的实例。与之相对的是,如果输入有一些小的变化,一个拥有大权重的网络会大幅改变其行为来响应变化。因此一个未正则化的网络可以利用大权重来学习得到训练集中包含了大量噪声信息的复杂模型。概括来说,正则化网络能够限制在对训练数据中常见数据构建出相对简单的模型,并且对训练数据中的各种各样的噪声有较好的抵抗能力。所以我们希望它能使我们的网络真正学习到问题中的现象的本质,并且能更好的进行泛化。
按照这种说法,你可能会对这种更倾向简单模型的想法感到紧张。人们有时把这种想法称作「奥卡姆剃刀」,并且就好像它是科学原理一样,热情地应用它。然而,它并不是一个普遍成立的科学原理。并不存在一个先验的符合逻辑的理由倾向于简单的模型,而不是复杂的模型。实际上,有时候更复杂的模型反而是正确的。
让我介绍两个正确结果是复杂模型的例子吧。在 1940 年代物理学家马塞尔施恩(Marcel Schein)宣布发现了一个新的自然粒子。他工作所在的通用电气公司欣喜若狂并广泛地宣传了这一发现。但是物理学家汉斯贝特(Hans Bethe)却怀疑这一发现。贝特拜访了施恩,并且查看了新粒子的轨迹图表。施恩向贝特一张一张地展示,但是贝特在每一张图表上都发现了一些问题,这些问题暗示着数据应该被丢弃。最后,施恩向贝特展示了一张看起来不错的图表。贝特说它可能只是一个统计学上的巧合。施恩说「是的,但是这种统计学巧合的几率,即便是按照你自己的公式,也只有五分之一。」贝特说「但是我们已经看过了五个图表。」最后,施恩说道「但是在我的图表上,每一个较好的图表,你都用不同的理论来解释,然而我有一个假设可以解释所有的图表,就是它们是新粒子。」贝特回应道「你我的学说的唯一区别在于你的是错误的而我的都是正确的。你简单的解释是错的,而我复杂的解释是正确的。」随后的研究证实了大自然是赞同贝特的学说的,之后也没有什么施恩的粒子了1。
另一个例子是,1859 年天文学家勒维耶(Urbain Le Verrier)发现水星轨道没有按照牛顿的引力理论,形成应有的形状。它跟牛顿的理论有一个很小很小的偏差,一些当时被接受的解释是,牛顿的理论或多或少是正确的,但是需要一些小小的调整。1916 年,爱因斯坦表明这一偏差可以很好地通过他的广义相对论来解释,这一理论从根本上不同于牛顿引力理论,并且基于更复杂的数学。尽管有额外的复杂性,但我们今天已经接受了爱因斯坦的解释,而牛顿的引力理论,即便是调整过的形式,也是错误的。这某种程度上是因为我们现在知道了爱因斯坦的理论解释了许多牛顿的理论难以解释的现象。此外,更令人印象深刻的是,爱因斯坦的理论准确的预测了一些牛顿的理论完全没有预测的现象。但这些令人印象深刻的优点在早期并不是显而易见的。如果一个人仅仅是以朴素这一理由来判断,那么更好的理论就会是某种调整后的牛顿理论。
这些故事有三个意义。第一,判断两个解释哪个才是真正的「简单」是一个非常微妙的事情。第二,即便我们能做出这样的判断,简单是一个必须非常谨慎使用的指标。第三,真正测试一个模型的不是简单与否,更重要在于它在预测新的情况时表现如何。
谨慎来说,经验表明正则化的神经网络通常要比未正则化的网络泛化能力更好。因此本书的剩余部分我们将频繁地使用正则化。我举出上面的故事仅仅是为了帮助解释为什么还没有人研究出一个完全令人信服的理论来解释为什么正则化会帮助网络泛化。事实上,研究人员仍然在研究正则化的不同方法,对比哪种效果更好,并且尝试去解释为什么不同的方法有更好或更差的效果。所以你可以看到正则化是作为一种「杂牌军」存在的。虽然它经常有帮助,但我们并没有一套令人满意的系统理解为什么它有帮助,我们有的仅仅是没有科学依据的经验法则。
这存在一个更深层的问题,一个科学的核心问题。就是我们怎么去泛化这一问题。正则化可以给我们一个计算魔法棒来帮助我们的网络更好的泛化,但是它并没有给我们一个原则性的解释泛化是如何工作的,也没有告诉我们最好的方法是什么。
这尤其令人烦恼,因为在日常生活中,我们人类有很好的泛化现象的能力。给一个孩子看几张大象的图片,他就能很快地学习并辨认出其它大象。当然,他们偶尔也会犯错,也许会无法区分一个犀牛和一个大象,但是总体来说这个过程非常的准确。因此我们有一个系统——人的大脑——拥有大量的自由变量。对这个系统展示一张或几张训练图片之后,这个系统就可以学习并泛化其它的图片。我们的大脑在某种程度上,正则化得非常好!我们是怎么做到的?目前我们还不知道。我预计未来几年人工神经网络领域将开发出更强大的正则化技术,这些技术能使神经网络能更好地泛化,即使数据集非常小。
事实上,我们的网络已先天地泛化得很好。一个具有 100 个隐层神经元的网络有近 80,000 个参数。而我们的训练数据中只有 50,000 个图像。这就好比试图将一个 80,000 次多项式拟合为 50,000 个数据点。按理来说,我们的网络应该退化得非常严重。然而,正如我们所见,这样一个网络事实上泛化得非常好。为什么会是这样?这不太好理解。据推测2说「多层网络中的梯度下降学习的过程中有一个『自我正则化』效应」。这是非常意外的好处,但是这也某种程度上让人不安,因为我们不知道它是怎么工作的。与此同时,我们将采用一些更务实的方法并尽可能地应用正则化。我们的神经网络将会因此变得更好。
最后,让我说明一个之前没有解释到的细节:我们的 L2 正则化没有约束偏置(biases)。当然,通过修改正则化过程来正则化偏置会很容易。但根据经验,这样做往往不能较明显地改变结果。所以在一定程度上,是否正则化偏置仅仅是一个习惯问题。然而值得注意的是,有一个较大的偏置并不会使得神经元对它的输入像有大权重那样敏感。所以我们不用担心较大的偏置会使我们的网络学习训练数据中的噪声。同时,允许大规模的偏置使我们的网络在性能上更为灵活——特别是较大的偏置使得神经元更容易饱和,这通常是我们期望的。由于这些原因,我们通常不对偏置做正则化。
1 这个故事来自于物理学家 Richard Feynman 和 历史学家 Charles Weiner 的一次访谈中。
2 Gradient-Based Learning Applied to Document Recognition, Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner (1998)