神经网络的结构
下一章我将介绍一个能够良好分类手写数字的神经网络。在那之前,解释一些描述网络不同部分的术语是很有必要的。假设我们有如下网络:
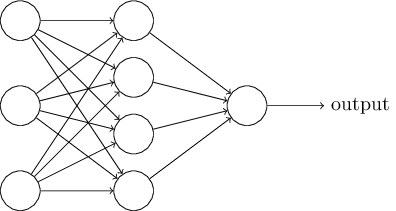
如前所述,网络中最左边的一层被称作输入层,其中的神经元被称为输入神经元(input neurons)。最右边的一层是输出层(output layer),包含的神经元被称为输出神经元(output neurons)。在本例中,输出层只有一个神经元。网络中间的一层被称作隐层(hidden layer),因为它既不是输入层,也不是输出层。「隐」这个字听起来似乎有点神秘的感觉——当我第一次听到这个字时认为其必然包含着深刻的哲学或数学含义——然而除了「既非输入、又非输出」这个含义外,它真的没有别的意思了。上面的网络只有一个隐层,然而在一些网络中往往有多个隐层。比如下面图示的4层网络就有两个隐层:
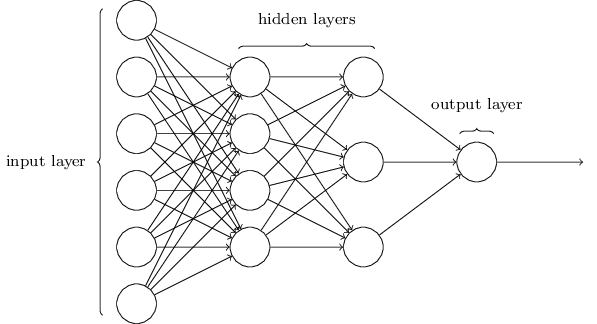
由于历史原因,这些多层网络有时又被称为多层感知机(multilayer perceptron,MLP),这多少有些混淆,因为这些网络都是由sigmoid神经元构成的,而非感知机。在本书中我不准备使用MLP这个术语,因为我觉得这会带来困惑,在这里只想提醒读者这个名词的存在。
网络的输入输出层设计是比较直观的。比如说,假如我们尝试判断一张手写数字图片上面是否写着「9」。很自然地,我们将图片像素的灰度值作为网络的输入。假设图片是的灰度图像,那么我们需要个输入神经元,每个神经元接受规格化的到间的灰度值。输出层只需要包含一个神经元,当输出值小于时说明「输入图片不是9」,否则表明「输入图片是9」。
相对于输入输出层设计的直观,隐层的设计就是一门艺术了。特别的,单纯地把一些简单规则结合到一起来作为隐层的设计是不对的。事实上,神经网络的研究者们已经总结了很多针对隐层的启发式设计规则,这些规则能够用来使网络变得符合预期。举例来说,一些启发式规则可以用来帮助我们在隐层层数和训练网络所需的时间开销这二者间找到平衡。在书的后面部分我们就将遇到一些启发式设计规则。
到目前为止,我们讨论的都是前馈神经网络(feedforward neural networks),即把上一层的输出作为下层输入的神经网络。这种网络是不存在环的——信息总是向前传播,从不反向回馈。如果我们要制造一个环,那么我们将会得到一个使函数输入依赖于其输出的网络。这很难去理解,所以我们并不允许存在这样的环路。
但是,我们也有一些存在回馈环路可能性的人工神经网络模型。这种模型被称为递归神经网络(recurrent neural networks)。该模型的关键在于,神经元在变为非激活态之前会在一段有限时间内均保持激活状态。这种激活状态可以激励其他的神经元,被激励的神经元在随后一段有限时间内也会保持激活状态。如此就会导致更多的神经元被激活,一段时间后我们将得到一个级联的神经元激活系统。在这个模型中环路并不会带来问题,因为神经元的输出只会在一段之间之后才影响到它的输入,它并非实时的。
递归神经网络比起前馈神经网络影响力小很多,一部分原因是递归神经网络的学习算法还不够强大,至少目前是如此。不过递归神经网络依然非常有吸引力。从思想上来看它要比前馈神经网络更接近我们大脑的工作方式。而且递归神经网络也可能解决一些重要的、前馈神经网络很难处理的问题。不过为控制篇幅,本书将主要关注更广泛应用的前馈神经网络。