过拟合和正则化
当某个数学模型被一些物理学家应用到了一个悬而未决的重要的物理问题上时,诺贝尔物理学奖获得者恩里科·费米(Enrico Fermi)被问及对于此举的观点。虽然模型与实验结果契合的很好,但费米还是对此有所怀疑。他问道「在这个模型中有多少个可以自由设置的参数」,他得到的答案是「4 个」。费米回复说1「我的朋友约翰尼·冯诺依曼(Johnny von Neumann)常说,他用四个参数可以模拟一头大象,用五个可以使它摇动鼻子。」
费米的这个观点是在表明:有大量自由参数的模型能够描述一个足够宽泛的现象。即使这样的模型与现有的数据吻合得很好,这也不能说它是一个好的模型。这仅仅只能说明,有足够自由度的模型基本上可以描述任何给定大小的数据集,但是它并没有真正地洞察到现象背后的本质。这就会导致该模型在现有的数据上表现得很好,但是却不能普及到新的情况上。判断一个模型真正好坏的方法,是看其对未知情况的预测能力。
费米和冯诺伊曼对持有四个参数的模型都抱有怀疑的态度。然而我们分类 MNIST 数字所用的个隐藏神经元网络就有将近个特征!这个数量非常庞大。个隐藏神经元网络有接近个特征,最先进的深度神经网络或许包含数百万,甚至数亿计的特征。我们应该相信这些结果吗?
下面让我们来举个例子来突出问题的严重性。我们会制造出一种情况,使我们的网络不能够很好地适应新数据。假设我们使用有个隐藏神经元网络,其中含有个特征。但是不用全部的个 MINST 图像做训练,而仅仅使用前个。用较小的训练集能够使突出泛化的问题。此外,我们依然用交叉熵代价函数来训练模型,学习率为,mini-batch 的大小选为。然而,与之前不同的是,我们将要迭代次,由于使用了较少的训练实例,所以就要较多的训练次数。让我们用 network2 看一下代价函数的变化趋势:
>>> import mnist_loader
>>> training_data,validation_data,test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10],cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000],400,10,0.5,evaluation_data=test_data,
... monitor_evaluation_accuracy=True,monitor_training_cost=True)
根据结果,我们能绘制网络学习成本的变化趋势2:
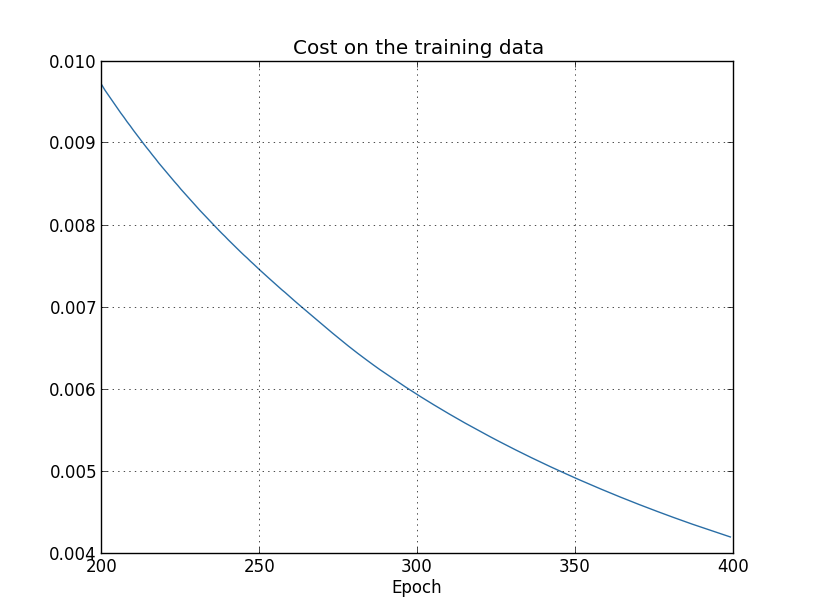
正如我们期望的那样,代价在平滑地下降。请注意,图中仅仅展示了第次迭代到第次迭代的阶段。我们能够从此判断出之后阶段的学习趋势。我们稍后会看到,后面的阶段是真正有趣的地方所在。
现在让我们来看看测试数据上的分类准确率随着时间是怎样变化的:
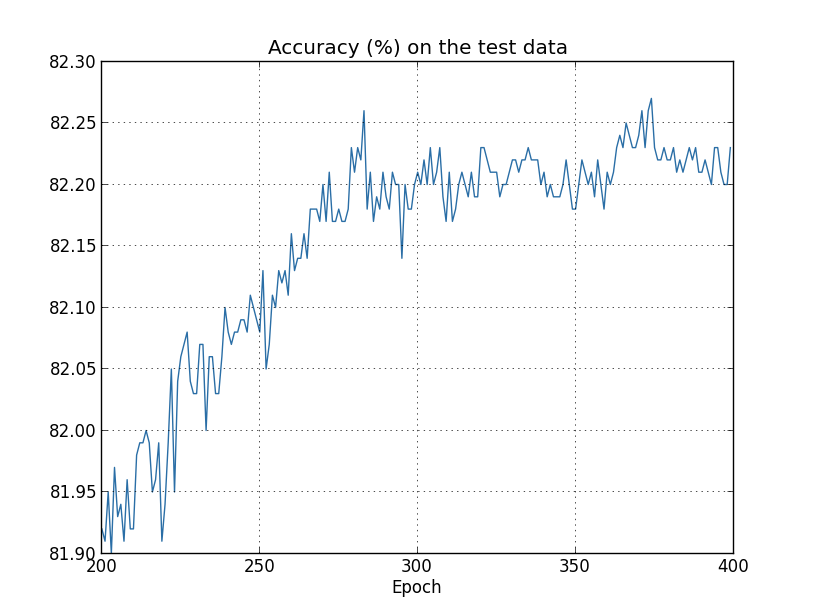
同样,我选取了图表的一部分。在前步(未显示)准确率上升到接近百分之。然后学习的效果就逐渐放缓。最后,在步附近,分类准确率几乎停止改善。之后的学习仅仅在步就达到的准确率附近有一些小的随机波动。与上一个图表对比,我们会发现,训练数据的代价函数值是持续下降的。如果我们只关注代价函数,模型似乎一直在“改进”。但测试精度结果表明:此时的改进只是一种错觉。正如费米所不喜欢的模型那样,在步之后,我们网络的学习不能够再很好地推广到测试数据上。所以此时的学习是无用的。在步之后,我们称此时的网络是过拟合(overfitting)或过训练(overtraining)的。
你也许在猜测问题是否出在我关注着训练数据的代价函数,却期待着测试数据的分类准确率,这两个指标完全是风马牛不相及。如果我们选择比较训练数据的代价和测试数据的代价会发生什么呢?这两个同类的指标总可以比较吧?或者我们比较训练数据和测试数据的分类精度又会怎样呢?事实上,无论我们选取什么指标作比较,本质上都会产生同样的结果。不信的话,让我们来看看测试数据的代价变化:
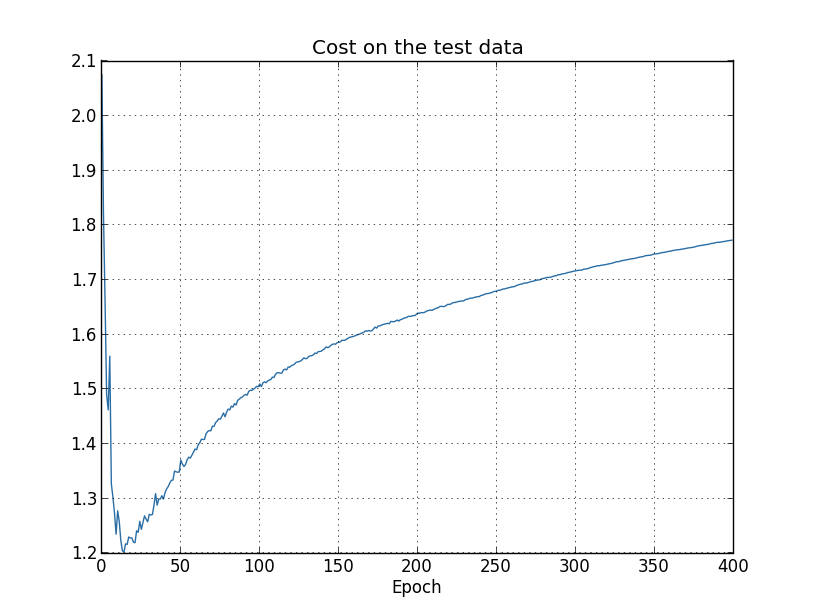
从图中可以看到,测试数据的代价在步前一直在降低,之后它开始变大,然而训练数据的代价是在持续降低的。这是另外一个能够表明我们的模型是过拟合的迹象。而此时,我们遇到了一个难题,到底哪一个才是发生过拟合的关键点,步还是步?从实际应用的角度来看,我们真正关心的是提高测试数据的分类精度,而测试数据的代价只不过是分类精度的附属品。因此,在我们的神经网络中,把步视为模型开始过拟合的转折点。
在训练数据的分类精度中也可以看到过拟合的迹象:
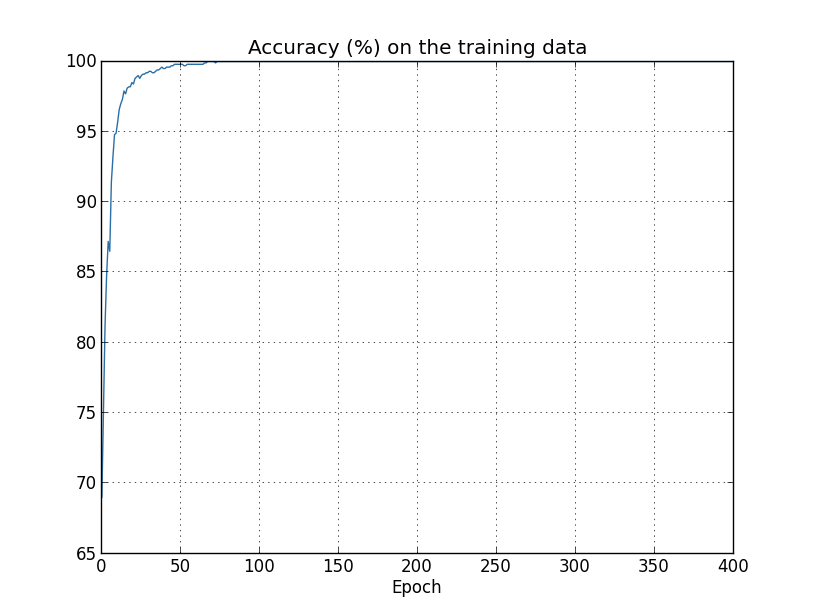
准确率一直上升到百分之。也就是说,网络能正确分类所有个训练图像!而与此同时,测试准确率仅为百分之。所以我们的网络只是在学习训练集的特性,而不能完全识别普通的数字。就好像网络仅仅是在记忆训练集,而没有真正理解了数字能够推广到测试集上。
过拟合是神经网络中一个主要的问题。尤其是在含有大量权重和偏差参数的现代网络中。为了更有效地训练,我们需要一种能够检测过拟合发生时间的方法,这样就不会发生过度训练。此外,我们也需要一种能减少过拟合影响的技术。
检测过拟合一个显而易见的方法就是如上面提到的,跟踪网络训练过程中测试数据的准确率。如果测试数据的精度不再提高,就应该停止训练。当然,严格地说,这也不一定就是过拟合的迹象,也许需要同时检测到测试数据和训练数据的精度都不再提高时才行。当然,这个策略是能够避免过拟合的。
事实上,我们将采用这种策略的一个变种。回想一下,我们曾载入了三个 MNIST 数据集:
>>> import mnist_loader
>>> training_data,validation_data,test_data = \
... mnist_loader.load_data_wrapper()
到目前为止,我们一直在使用 training_data 和 test_data,忽视了 validation_data。validation_data 包含张与 张 training_data 和张 test_data 图像不同的 MNIST 数字图像。我们将使用 validation_data 而不是 test_data 来预防过拟合。为了做到这一点,将使用与上面 test_data 相同的方法。也就是说,在每一步训练之后,计算 validation_data 的分类精度。一旦 validation_data 的分类精度达到饱和,就停止训练。这种策略叫做提前终止(early stopping)。当然在实践中,我们并不能立即知道什么时候准确度已经饱和。取而代之,我们在确信精度已经饱和之前会一直训练3。
为什么要用 validation_data 而不是 test_data 来防止过拟合呢?通过 validation_data 来选择不同的超参数(例如,训练步数、学习率、最佳网络结构、等等)是一个普遍的策略。我们通过这样的评估来计算和设置合适的超参数值。虽然我到现在才提到超参数,但其实我在之前就已经提到怎样选择超参数了。(后面会介绍更多)
当然,上面的解释不能回答为什么我用 validation_data 而不是 test_data 来防止过拟合。实际上,更一般的问题是为什么用 validation_data 而不是 test_data 来设置超参数?当我们设置超参数时,有很多种不同的选择。如果基于 test_data 的评估结果设置超参数,有可能我们的网络最后是对 test_data 过拟合。也就是说,我们或许只是找到了适合 test_data 具体特征的超参数,网络的性能不能推广到其它的数据集。通过 validation_data 来设置超参数能够避免这种情况的发生。然后,一旦我们得到了想要的超参数,就用 `test_data``` 做最后的精度评估。这让我们相信test_data的精度能够真正提现网络的泛化能力。换句话说,你能把validation_data视为帮助我们学习合适超参数的一种训练数据。由于validation_data和test_data` 是完全分离开的,所以这种找到优秀超参数的方法被称为分离法(hold out method)。
如果我们在对 test_data 进行了性能评估后,我们突然改变主意想要尝试选择不同方法——例如另一种网络结构——其中需要也涉及一批新的超参数设置。如果我们这样做了,不也有可能导致模型对 test_data 过拟合吗?我们需要一个潜在的无限数据集来使我们的模型更有泛化能力吗?这是个很深刻很棘手的问题。不过,出于实践目的,我们不必有过多担心。仅仅用上面提到的,基于 training_data、validation_data 和 test_data 的分离法来解决就行。
目前为止,我们已经看过了只用张训练图片的过拟合状况。而当用全部的图片训练集时又会发生什么呢?保持相同的参数(个隐藏神经元,学习率为,mini-batch 的大小为),使用全部张图片,迭代次。下面是显示训练数据和测试数据分类精度的图表。注意我在这里用了测试数据,而不是验证数据,是为了与前面的图片做更直接的比较。
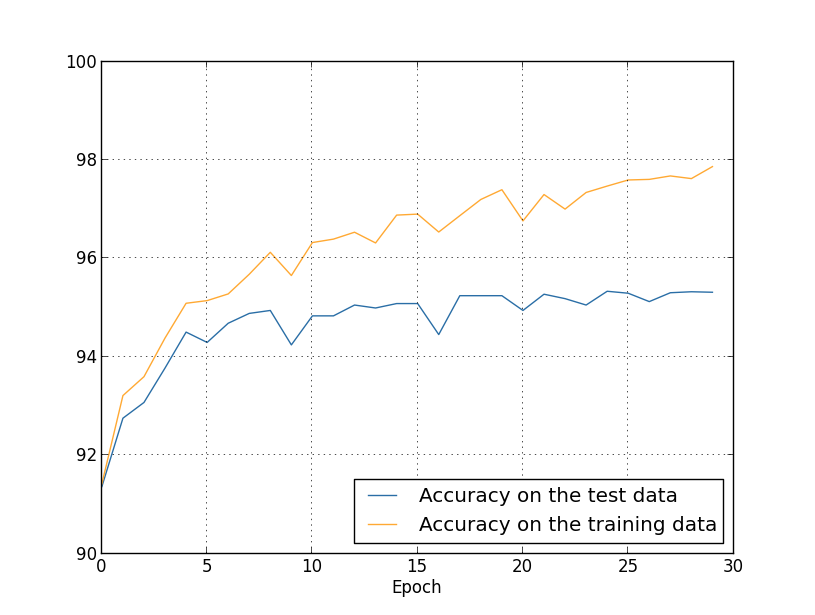
正如你看到的,相比使用张训练实例,使用张训练实例的情况下,测试数据和训练数据的准确率更加接近。特别地,训练数据上最高的分类精度百分之仅仅比测试数据的百分之高出个百分点。而之前有百分之的差距!虽然过拟合仍然存在,但已经大大降低了。我们的网络能从训练数据更好地泛化到测试数据。一般来说,增加训练数据的数量是降低过拟合的最好方法之一。即便拥有足够的训练数据,要让一个非常庞大的网络过拟合也是比较困难的。不幸的是,训练数据的获取成本太高,因此这通常不是一个现实的选择。
1引用来自Freeman Dyson的一篇精彩的文章。他曾提出了有缺陷的模型,四参数大象的例子可以在这里找到。
2本图和接下来四幅图都是通过运行overfitting.py产生的。
3它需要一些判断来决定何时停止。在前面的图表中,我挑选步作为精度饱和点。这有可能是过于悲观。神经网络在训练的过程中有时会停滞一段时间,然后才会接着改善。如果在步之后网络还能够继续学习,我也不会惊讶,不过,就算有任何进一步的提高,幅度可能都会很小。因此,或多或少地采取提前停止的激进策略是合理的。