正则化

避免过拟合的方法之一是增加训练数据数量。那么，还有没有别的方法能让我们避免过拟合呢？一种可能的方法是减小网络的规模。然而，我们并不情愿减小规模，因为大型网络比小型网络有更大的潜力。

幸好，哪怕使用固定的网络和固定的训练数据，我们还有别的方法来避免过拟合。这就是所谓的正则化（regularization）技术。在这一节我将描述一种最常用的正则化技术——权重衰减（weight decay）或叫 L2 正则（L2 regularization）。L2 正则的思想是，在代价函数中加入一个额外的正则化项。这是正则化之后的交叉熵：

$$\begin{eqnarray} C = -\frac{1}{n} \sum_{xj} \left[ y_j \ln a^L_j+(1-y_j) \ln (1-a^L_j)\right] + \frac{\lambda}{2n} \sum_w w^2. \tag{85}\end{eqnarray}$$

第一项是常规的交叉熵表达式。但我们加入了第二项，也就是网络中所有权值的平方和。它由参数 $\lambda / 2n$ 进行调整，其中 $\lambda > 0$ 被称为正则化参数（regularization parameter），$n$ 是我们训练集的大小。我稍后会讨论应该如何选择 $\lambda$。另外请注意正则化项不包括偏置。我稍后也会提到这点。

当然，我们也可以对其它的代价函数进行正则化，例如平方代价。正则化的方法与上面类似：

$$\begin{eqnarray} C = \frac{1}{2n} \sum_x \|y-a^L\|^2 + \frac{\lambda}{2n} \sum_w w^2. \tag{86}\end{eqnarray}$$

在两种情况中，我们都能把正则化的代价函数写成：

$$\begin{eqnarray} C = C_0 + \frac{\lambda}{2n} \sum_w w^2, \tag{87}\end{eqnarray}$$

其中 $C_0$ 是原本的、没有正则化的代价函数。

直观来说，正则化的作用是让网络偏好学习更小的权值，而在其它的方面保持不变。选择较大的权值只有一种情况，那就是它们能显著地改进代价函数的第一部分。换句话说，正则化可以视作一种能够折中考虑小权值和最小化原来代价函数的方法。两个要素的相对重要性由 $\lambda$ 的值决定：当 $\lambda$ 较小时，我们偏好最小化原本的代价函数，而 $\lambda$ 较大时我们偏好更小的权值。

为什么这种折中能够减少过拟合，其中的原因也太不明显了！但事实是它的确能够减少过拟合。我们将在下一部分阐述为何这样的折中能够减少过拟合。先让我们通过一个例子展示正则化确实能够减小过拟合。

为了构建这样一个例子，我们首先要解决如何把随机梯度下降学习算法应用于正则化的神经网络中。我们尤其需要知道如何对网络中所有的权值和偏置计算偏导数 $\partial C / \partial w$和$\partial C / \partial b$。对等式（87）求偏导可得：

$$\begin{eqnarray} \frac{\partial C}{\partial w} & = & \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \tag{88}\\ \frac{\partial C}{\partial b} & = & \frac{\partial C_0}{\partial b}. \tag{89}\end{eqnarray}$$

正如上一章所述，其中 $\partial C_0 / \partial w$ 和 $\partial C_0 / \partial b$ 可由反向传播计算。于是我们发现计算正则化代价函数的梯度相当简单：只要照常使用反向传播，并把 $\frac{\lambda}{n} w$ 加到所有权值项的偏导数中。偏置的偏导数保持不变，所以偏置的梯度下降学习的规则保持常规的不变：

$$\begin{eqnarray} b & \rightarrow & b -\eta \frac{\partial C_0}{\partial b}. \tag{90}\end{eqnarray}$$

而对于权值的学习规则变为：

$$\begin{eqnarray} w & \rightarrow & w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w \tag{91}\\ & = & \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w}. \tag{92}\end{eqnarray}$$

其它部分与常规的梯度下降学习规则完全一样，不一样的地方是我们以 $1-\frac{\eta \lambda}{n}$ 调整权值 $w$。这种调整有时也被称作权重衰减（weight decay），因为它减小了权重。一眼看去权值将被不停地减小直到为 0。但实际上并不是这样的，因为如果可以减小未正则化的代价函数的话，式中的另外一项可能会让权值增加。

好的，这就是梯度下降实现的方法。那么随机梯度下降呢？和未正则化的随机梯度下降一样，我们首先在包含 $m$ 个训练样例的 mini-batch 数据中进行平均以估计 $\partial C_0 / \partial w$ 的值。因此对于随机梯度下降法而言正则化的学习方法就变成了（参考等式 （20））：

$$\begin{eqnarray} w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w}, \tag{93}\end{eqnarray}$$

其中的求和是对 mini-batch 中的所有训练样例进行的，$C_x$ 是每个样例对应的未正则化的代价。这与通常的随机梯度下降方法一致，除了权重衰减变量 $1-\frac{\eta \lambda}{n}$。最后，为了表述完整，我要说明对于偏置的正则化学习规则。毫无疑问，那就是与未正则化的情况（如等式 （21））完全一样，

$$\begin{eqnarray} b \rightarrow b - \frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial b}, \tag{94}\end{eqnarray}$$

其中的求和是对 mini-batch 中的所有训练样例 $x$ 进行的。

让我们看看正则化如何改变了我们的神经网络的表现。我们将使用一个神经网络来进行验证，其包含 $30$ 个隐藏神经元，mini-batch 大小为 $10$，学习率为 $0.5$，并以交叉熵作为代价函数。然而，这次我们设置正则化参数 $\lambda = 0.1$。注意在代码中，我们使用变量名 lmbda，因为 lambda 是 Python 的保留字，其含义与此无关。我也再次使用了 test_data 而非 validation_data。严格来说，我们应该使用 validation_data，详细原因我们在此前已经解释过。不过我决定用 test_data 因为它能让结果与我们此前未正则化的结果进行更直观的比较。对代码稍作改动你即可使用 validation_data，并且你将发现得到的结果很相似。

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10](), cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000](), 400, 10, 0.5,
... evaluation_data=test_data, lmbda = 0.1,
... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True,
... monitor_training_cost=True, monitor_training_accuracy=True)

代价函数一直都在下降，几乎与此前在未正则化的情形一样¹：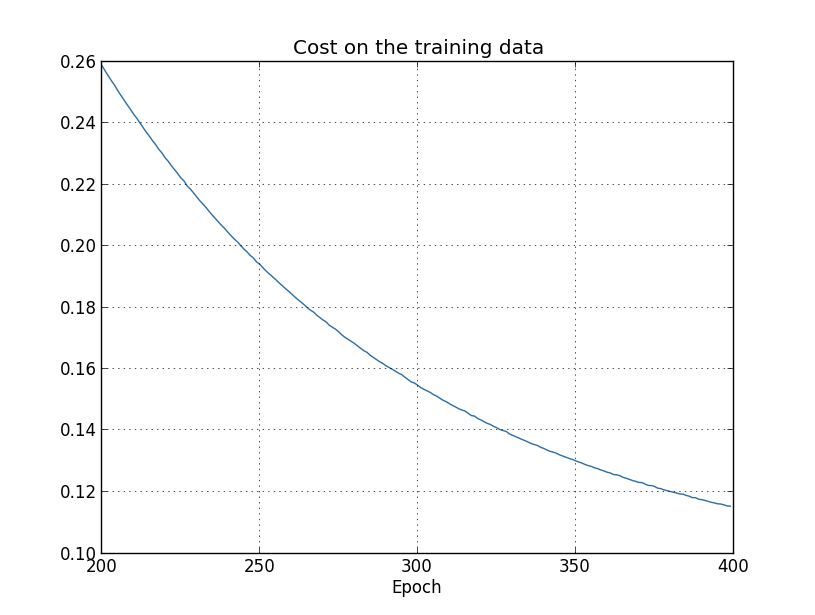

但这次它在 test_data 上的准确率在 400 次迭代中保持提升：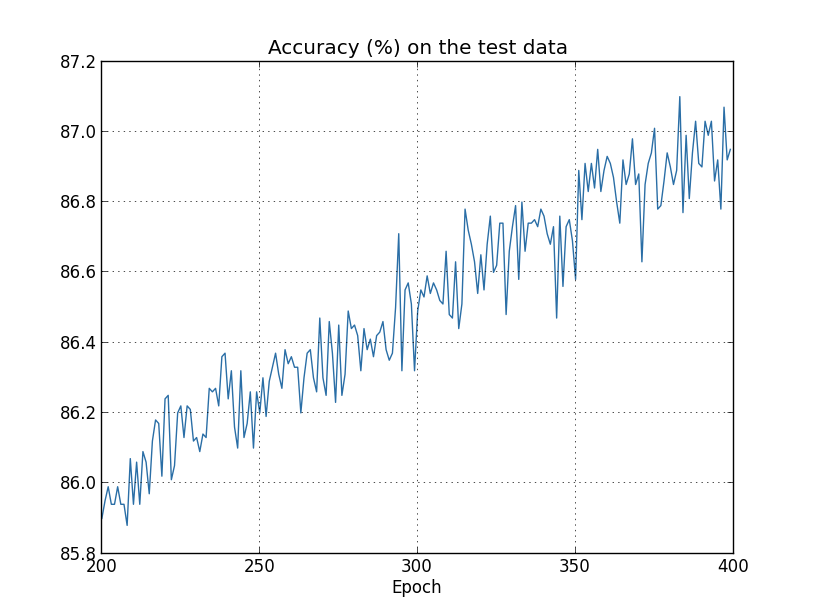

显然，应用正则化抑制了过拟合。同时，准确率也显著提升了：分类准确率峰值为 $87.1%$，更高于未正则化例子中的峰值 $82.27%$。实际上，我们几乎确定，继续进行迭代可以得到更好的结果。从经验来看，正则化让我们的网络生成得更好，并有效地减弱了过拟合效应。

如果我们从仅有 $1000$ 张训练图片迁移到有着 $50000$ 张图片的环境，结果又会怎么样呢？当然，我们已经看到过拟合对于 $50000$ 张图片来说不再是个大问题了。那么正则化能在这上面提供更多帮助吗？让我们把超参数保持跟以前的一样：$30$ 次迭代，学习率为 $0.5$，mini-batch 数目为 $10$。然而，我们需要调整正则化参数。原因是，训练数据集的大小已经从 $n = 1000$ 变成了 $n = 50000$，而这就改变了权重衰减因数 $1 - \frac{\eta \lambda}{n}$。如果我们继续使用 $\lambda = 0.1$ 那么权重衰减将会大大减小，而正则化的效果也会相应减弱。我们调整 $\lambda = 5.0$ 以进行补偿。
好的，让我们训练我们的网络，并在此之前重新初始化权值：

>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5,
... evaluation_data=test_data, lmbda = 5.0,
... monitor_evaluation_accuracy=True, monitor_training_accuracy=True)

我们得到结果如图：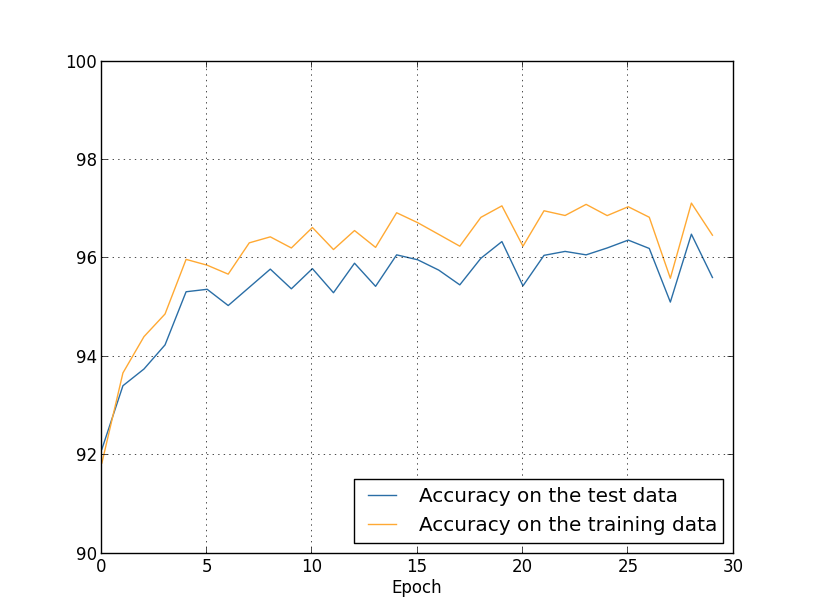

这里有很多好消息。首先，我们在测试数据上的分类准确率提升了，从未正则化时的百分之 $95.49$ 到百分之 $96.49$。这是一个重大的提升。第二，我们能看到训练数据的结果与测试数据的之间的间隙相比之前也大大缩小了，在一个百分点之下。虽然这仍然是一个明显的间隙，但我们显然已经在减弱过拟合上做出了大量的提升。

最后，让我们看看当我们使用 $100$ 个隐藏神经元并设置 $\lambda = 5.0$ 时测试分类准确率。我将不会对这里的过拟合进行详细的分析，这只是纯粹为了有趣，只为了看看我们使用新的技巧——交叉熵代价函数和L2 正则化——能让我们得到多高的准确率。

>>> net = network2.Network([784, 100, 10](),\
... cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0,\
... evaluation_data=validation_data,\
... monitor_evaluation_accuracy=True)

最终结果是，分类准确率在验证数据上达到了 $97.92%$。相对于 $30$ 个隐藏神经元的情形，这是一个飞跃。事实上，只要再训练更多些，保持 $\eta = 0.1$ 和 $\lambda = 5.0$，增加到 $60$ 次迭代，我们能够突破百分之 $98$ 的壁垒，在验证数据上达到百分之 $98.04$ 的准确率。对于这 152 行代码来说是不错的结果了！

我已经描述了正则化作为一种减弱过拟合并提升分类准确率的方法。事实上，这并不是它唯一的好处。经验表明，当在多次运行我们的 MNIST 网络，并使用不同的（随机）权值初始化时，我发现未正则化的那些偶尔会被「卡住」，似乎陷入了代价函数的局部最优中。结果就是每次运行可能产生相当不同的结果。相反，正则化的那些的每次运行可以提供更容易复现的结果。

为什么会这样呢？启发式地来说，如果代价函数没有正则化，那么权重向量的长度倾向于增长，而其它的都不变。随着时间推移，权重向量将会变得非常大。这可能导致权重向量被限制得或多或少指向同一个方向，因为当长度过长时，梯度下降只能带来很小的变化。我相信这一现象令我们的学习算法难于恰当地探索权重空间，因而难以给代价函数找到一个好的极小值。

¹ 这张图和下两张图的结果是由程序 overfitting.py 产生的。